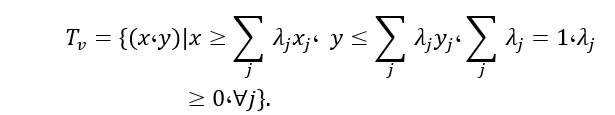تحلیل پوششی داده ها یک چارچوب تئوریک را برای تحلیل و سنجش عملکرد و اندازه گیری کارایی یک سازمان فراهم می آورد. روش مذکور شامل مجموعه ای از تکنیک های برنامه ریزی خطی است که مرز کارا، را با استفاده از داده های مشاهده شده بنا می کند. آنگاه به ارزیابی و اندازه گیری کارایی واحدهای تصمیم گیرنده می پردازد. از این رو در ادامه این فصل به بررسی و معرفی دقیقتر این روش می پردازیم.
انسان در تمام قرون و اعصار هميشه با مشكلي به نام محدوديت و كميابي مواجه بوده است. اين محدوديت و كميابي در تمام زمينه ها از جمله عوامل توليد و به تبع آن كالاها و خدمات كاملا محسوس است. از اين رو، كوششهاي اقتصادي انسان همواره معطوف بر آن بوده كه حداكثر نتيجه را با كمترين امكانات و عوامل موجود به دست آورد. از طرفي تداوم بقاي واحدها و سازمانها در هر نظام اقتصادي در گرو ايجاد ارزش افزوده است. براي دستيابي به اين مهم تنها داشتن منابع كافي نيست، بلكه نحوه تركيب و استفاده از منابع اهميت به سزايي دارند كه اين مهم خود در گرو طرز عمل و نحوه كار در سازمانها مي باشد. استفاده از ابزارهاي علمي سنجش كارايي و بهره وري می تواند ارائه كننده اطلاعات مفيد براي مديريت جهت تصميم گيري به منظور بهبود شيوه هاي انجام فعاليت و بكارگيري منابع باشد. امروزه با وجود فضاي رقابتي، سازما نها علاوه بر اينكه بايد بتوانند با منابع موجود به مقدار مورد نياز توليد كنند، بايد اين توانايي را داشته باشند كه فرايند توليد را به گونه اي پيش ببرند كه بتوانند از رقبا پيشي بگيرند تا به حيات خود ادامه دهند. به همين دليل سازمان ها با به كارگيري روشهايي كه در جهت ارزيابي عملكردشان مي باشد ضعفها و قوتها، فرصتها و تهديدها را براي بهبود و اصلاح روشها نمايان مي سازند.
ارزیابی کارایی واحدهاي خدماتی، تولیدي، آموزشی و … همواره مسأله مهمی نزد مهندسان و اقتصاددانان بوده است. اینکه یک واحد چگونه از مجموعه امکاناتی که در اختیار دارد استفاده نموده و طی یک دوره مورد بررسی چگونه عملکردي داشته، سؤالی است که در حیطه ارزیابی کارایی می گنجد.
محدودیت عوامل تولید موجب گردیده است که توجه انسان به کارایی هرچه بیشتر در تمام فعالیتها و اقداماتی که به عمل می آورد به یک پدیده دائمی و مقبول نظر همگان مبدل شود. از این رو، در اقتصاد ملی هر جامعه ای کارایی و ارتقاء آن از جمله موضوعات برخوردار از اولویت قلمداد می گردد.
در محیط رقابتی امروز که دوام و بقاي سازمان ها به کیفیت تصمیمات ذینفعان بستگی دارد ارزیابی عملکرد از اهمیت قابل توجهی برخوردار بوده و نقش مهمی در بهبود عملکرد سازمان ها خواهد داشت. ارزیابی عملکرد بایستی از چنان جامعیتی برخوردار باشد که بتواند تمامی ابعاد پیرامون مترتب بر فعالیت سازمانها را با عملکرد آنها مرتبط نموده و نقش تصمیمات مدیران در نیل به اهداف و ارتقا عملکرد آنها را منعکس نماید.
كارايي بخشي از بهره وري است و به صورت هاي گوناگوني تعريف مي شود. ولي در يك مفهوم ساده شامل نسبت ستانده به نهاده در يك سيستم مي باشد. در تعريف ديگر كارايي، به صورت نسبت حداقل هزينه ممكن به هزينه تحقق يافته براي ارائه ميزان مشخص ستاده در مقايسه با ساير واحدهاي موجود در آن صنعت در نظر گرفته مي شود. كارايي مقياس، كارايي فني، كارايي تخصيصي، كارايي اقتصادي و كارايي قيمت، انواع مختلف كارايي هستند و همه آنها براي حداكثر كردن توليد با هزينه مشخص يا حداقل نمودن هزينه با سطح توليد مشخص هستند و نتيجه آنها نيز حداكثر كردن سود واحد تصميم گيرنده است.
مفهوم كارايي عمدتا در سه حوزه مهندسي، مديريت و اقتصاد مطرح است. در اقتصاد، مفهوم كارايي، همان تخصيص بهينه منابع است. هر چند كه از نظر اهداف كاربردي، تعاريف گوناگوني از كارايي عنوان شده است ، اما به طور كلي مي توان گفت كه كارايي، معرف نسبت ستاده ها به نهاده ها در مقايسه با يك استاندارد مشخص است. از طرفي ديگر، در حوزه علم مديريت علاوه بر سرمايه هاي فيزيكي، سرمايه هاي انساني نيز به عنوان نهاده هايي مهم و تعيين كننده در نظر گرفته مي شوند. لذا از آن جا كه كارايي افراد – با توجه به تشويق ها و تنبيه ها- ممكن است از توان افراد نيز بيشتر و يا كمتر شود، مقدار محاسبه شده براي آن ، محدود به مرز واحد نمي شود. به عبارت ديگر مي توان گفت كه كارايي، بهينگي استفاده از منابع در راستاي تامين اهداف كاركردي است.
از مقاله تحلیل پوششی داده ها دیدن کنید
از مقاله تحلیل پوششی داده ها دیدن کنید
از مقاله تحلیل پوششی داده ها دیدن کنید
عبارت است از توانايی بنگاه در بدست آوردن حداکثر تولید ممکن از مقدار مشخص عوامل تولید. این نوع کارآیی مفهومی نسبی است، زیرا مقایسه بین بنگاهها در نوع و نحوه استفاده از تکنولوژي است. در واقع کارآیی فنی عبارت است از حداکثر ستانده از مقدار معینی نهاده در سطوح ثابت تکنولوژي اگر یک تولید کننده بتواند مقدار معینی عامل تولید را بدون افزایش در مقادیر سایر عوامل کاهش دهد در حالی که همان سطح تولید را حفظ نماید، آن ترکیب از لحاظ فنی کارآ تلقی می شود . این نوع کارآیی ارتباط با قیمت عوامل ندارد بلکه مرتبط به حداقل کردن مقدار عوامل براي رسیدن به مقدار معینی محصول میباشد یا به عبارت دیگر تولید کننده بتواند بامقدار معینی نهاده بیشترین سطح تولید را داشته از نظر فنی کارآیی میباشد. حال قیمتهاي عوامل تولید هرچه که میخواهد باشد. لذا بنگاهی داراي کارآیی فنی بالاتري است که بتواند با مجموعه داده هاي مفروض و ثابت میزان محصول بیشتري را نسبت به سایر بنگاهها تولید نماید
عبارت است از توانایی یک بنگاه با توجه به قیمت هاي نسبی و تکنولوژي تولید استفاده از نهاده ها در نسبتهاي بهینه . به بیان دیگر میتوان گفت کارآیی تخصیصی نتیجه به کارگیري نهاده ها به نسبت مناسب می باشد که موجب میشود هزینه تولید حداقل گردد .
در تعاریف ساده کارآیی تخصیصی، تخصیصی است که صرفاً ناشی از اثر قیمتهاي نسبی عوامل تولید است و علت تغییر ترکیب استفاده از عوامل تولید وجود و یا تغییر قیمت عوامل تولید میباشد. به عبارت دیگر یک بنگاه که از نظر فنی کارآ میباشد ترکیبات مختلفی از عوامل تولید براي مقدار تولید مقدار معینی محصول میتواند داشته باشد که هزینه تولید آنها متفاوت است. در این صورت پیدا کردن ترکیبی از عوامل تولید که کمترین هزینه را براي مقدار معینی محصول دارا باشد کارآیی تخصیصی می گویند. نکته قابل توجه در مورد کارآیی تخصیصی این است که این نوع کارآیی زمانی وجود دارد که منابع بر اساس قیمتهاي بازار تخصیص یافته باشند و قیمتهاي عوامل معیار واقعی از کمیابی نسبی آنها باشد. این موردي است که قیمتها در بازار رقابت کامل تعیین شده باشند اما زمانی که قیمتها از طریق اثرات انحصاري تعریف شده باشند یقیناً نقش قیمتها در تخصیص منابع سود بخش نخواهد بود .(امام میبیدی، علی، (1379)، اصول اندازهگیری کارای و بهرهوری
از حاصلضرب کارآیی فنی در کارآیی تخصیصی کارآیی اقتصادي به دست میآید. در واقع کارآیی اقتصادي را میتوان توانایی بنگاه در به دست آوردن حداکثر سود ممکن با توجه به قیمتها و سطوح نهاده ها داشت .
کارآیی ساختاري یک صنعت از متوسط وزنی کارآیی شرکتهاي آن صنعت به دست میآید. با استفاده از معیار کارآیی ساختاري میتوان کارآیی صنایع مختلف با محصولات متفاوت را مقایسه کرد .
کارآیی مقیاس یک واحد از نسبت کارآیی مشاهده شده آن واحد به کارآیی در مقیاس بهینه به دست می آید هدف این کارآیی تولید در مقیاس بهینه میباشد .
در این حالت کارایی یک DMU مستقل از کارایی بقیه واحدها محاسبه می شود و از مقایسه یک واحد با استانداردهای کلی بدست می آید. چنان چه فرض شود برای واحدهای تصمیم گیرنده خاص استاندارد جهانی برای یک واحد ورودی، خروجی برابر Y* باشد، اگر واحد تصمیم گیرنده با مصرف یک واحد ورودی، واحد خروجی تولید کند، دراین صورت کارایی مطلق به صورت می باشد. یکی از بزرگترین محاسن کارایی مطلق این است که این نوع کارایی جایگاه واقعی واحدها را نشان می دهد.
در این حالت، کارایی هر واحد نسبت به کارایی بقیه واحدها سنجیده می شود. آنچه که باعث شده است عموما کارایی نسبی سازمان ها مدنظر پژوهشگران و اقتصاد دانان قرار بگیرد، فاصله زیاد واحدهای حقیقی بلاخص کشورهای جهان سوم با استانداردهای بین المللی است و ارائه راهکار برای رسیدن به سطح استاندارد غیر قابل اجرا خواهد بود و یا این که، چون در این نوع ارزیابی مقایسه با بیرون جامعه انجام می گیرد، از نظر بعضی مدیران غیر قابل قبول خواهد بود و الگوی حقیقی برای واحدهای ناکارا جهت کارا شدن وجود ندارد. بنابراین کارایی نسبی واحدها همواره کوچکتر یا مساوی یک است
حال چنان چه فرض کنیم واحد تصمیم گیرندهj ام، با صرف، خروجی را تولید نموده است، کارایی نسبی برای واحد Kام که آن را با نشان می دهیم، چنین تعریف می شود:
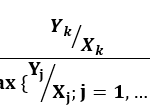
از جمله مزایای کارایی نسبی می توان به این مورد اشاره کرد که همواره یکی از واحدها دارای کارایی یک است.
تا اینجا کارایی را برای واحدهایی بررسی کردیم که یک ورودی ویک خروجی داشتند. حال چناچه فرض کنیم با واحدهایی روبه رو هستیم که با مصرف بردار ورودی ()، بردار خروجی ( را تولید می کنند. برای محاسبه کارایی چنین واحدهایی، اگر قیمت همه خروجی ها مشخص باشد و هزینه تمام ورودی ها معلوم باشد، کارایی آن از رابطه زیر بدست می آید، که در آن قیمت خروجی rام یعنی و هزینه ی ورودی iام یعنی می باشد و کارایی فوق به کارایی اقتصادی معروف است. اما در غیر این صورت، یعنی زمانی که نتوانیم ارزش مشخصی برای ورودی ها و خروجی ها درنظر بگیریم، برای تعیین وزنهای ورودی و خروجی ها، نیاز به استفاده از مدل های DEA داریم که در ادامه به ذکر آنها می پردازیم. در این حالت کارایی نسبی به صورت زیر محاسبه می شود:
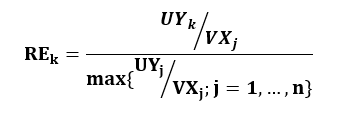
در واقع مزیت استفاده از مدلهای DEA این است که وزنهای ورودی ها و خروجی ها مستقل از نظر شخصی مدیر و توسط مدل مشخص می کند.
تعریف غالب بودن : با بردار های ورودی وخروجی (x,y) ، را غالب بر DMU با بردارهای (X,Y) می نامیم ، هرگاه:
در ادبیات موضوعه سنجش کارایی دو دسته مدل استفاده شده است دسته اول تحت عنوان روشهای پارامتری که بر پایه اصول اقتصاد سنجی است و دسته دوم تحت عنوان روشهای ناپارامتری است که مبتی بر مدلهای برنامه ریزی خطی می باشد و در ادامه تشریح می گردد
در روش های پارامتری که بیشتر بر پایه اصول اقتصادسنجی است و در اقتصاد مورد استفاده قرار می گیرد، ابتدا یک فرم تابعی (معمولا تابع تولید کاب– داگلاس) برای تابع تولید در نظر گرفته می شود. سپس پارامترهای تابع با استفاده از روشهای رگرسیونی برآورد می گردد. لازم به ذکر است که در روش های پارامتری علاوه بر محدودیت انتخاب تابع تولید، با محدودیت های دیگری نیز روبرو هستیم:
اول اینکه واحدها باید فقط یک محصول تولیدی داشته باشند و این در حالی است که ممکن است واحدهای تحت ارزیابی چند محصولی باشند.
دوم اینکه استفاده از روش کمترین مربعات برای برآورد پارامترهای تابع تولید بیان کاملی از نقاط ممکن تولید نمی باشد. زیرا تابع تولید بیشترین تولید ممکن به ازای هر ورودی است؛ در حالی که تابع محاسبه شده از این روش بیشترین تولید ممکن را در هر ورودی به دست نمی دهد. اولین مدل تخمین به روش پارامتری در سال 1977 توسط ایگنز لاول و اشمیت و همچنین میوزن و وان دن بروک ارایه شد. روش های پارامتری به دو گروه کلی قطعی و تصادفی تقسیم می شوند.
در تلاش برای رفع مشکلات موجود در روش های پارامتری روش های غیرپارامتری ایجاد شدند. فارل در سال 1967 اولین روش غیرپارامتری را جهت تعیین کارایی در حالت دو ورودی و یک خروجی ارایه نمود. وی بجای برآورد تابع تولید مرز کارای قطعه قطعه خطی را با اعمال فرض های زیر و با استفاده از تبدیل یک به یک
به دست آورد. شیب پاره خطها منفی یا صفر است و هیچ واحدی بین مرز و مبدا قرار نمی گیرد. نقاطی که روی مرز قرار می گیرند نقاط کارا و بقیه ناکارا هستند
در روشهاي ناپارامتري، تابع توليد برآورد نمي شود. مهمترين روش غيرپارامتري، روش تحليل پوششی داده ها (DEA) است و نیازی به تابع تولید براي تعيين كارايي نيست. اين روش توسط چارنز، کوپر و رودز ارائه شد و به مدل CCR معروف شد.
فرض کنید ميخواهيم كارايي چند واحد تصميم گيرنده (DMU) همگن را تعیین کنیم. اگر Xj، j=1..n ، نهاده ها یا به عبارت دیگر متغیرهای ورودی و Yj،i=1..m ستانده ها یا متغیرهای خروجی باشند، کارایی برابر است با:
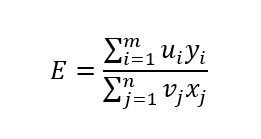
ui ضرآیب اهمیت ستانده ها و vj ضرایب اهمیت نهاده هاست. مسئله مهم تعیین این ضرایب است. گاهی این ضرایب مشخص، به عنوان مثال می تواند قیمت باشد و باید قیمت آنها را در نظر گرفت اما در بیشتر مواقع ممكن است قيمتها در دسترس نباشد يا نظرات متفاوتي در مورد اين ضرايب وجود داشته باشد. مدل CCR به نحو جالبی در این حالت مشکل ضرایب را حل می کند. آنها پیشنهاد کردند که هر واحد تصمیم گیرنده این ضرایب را می تواند به مقدار دلخواه اختیار کند، به شرط اینکه کارایی دیگر واحدها هم با این ضرایب محاسبه شود و و مقادیر کارایی نیز حدکثر برابر با یک باشد به عبارت دیگر برای بنگاه pام با فرض اینکه s واحد تصمیم گیرنده داشته باشیم، ماکزیمم مقدار کارایی را با تعیین ضرایب u و v چنان تعیین می کنیم که دیگر واحدها کارایی کمتر یا مساوی یک داشته باشند، یعنی:
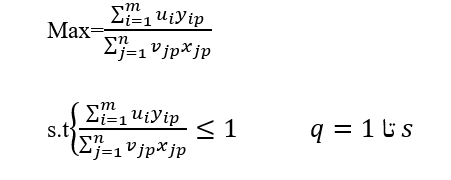
مدل فوق يك مدل برنامه ريزي غيرخطي است كه آن را مي توان به برنامه ريزي خطي تبديل كرد،
تحلیل پوششی دادهها یک روش برنامه ریزی ریاضی است که ابزار مناسب برای سنجش کارایی نسبی واحدهای تصمیم گیری ([1]DMU) در حالت چند ورودی و چند خروجی به حساب میآید. در سال 1978، چارنز[2]، کوپر[3] و رودز[4] با استفاده از برنامه ریزی ریاضی، روش ناپارامتری فارل را برای سیستمی با ورودیها و خروجیهای چند گانه تعمیم دادند و مدل معرفی شده آنها به نام مدل CCR معروف شد. سپس بنکر، چارنز و کوپر مدلCCR را برای حالت بازده به مقیاس متغیر تعمیم دادند و مدل پیشنهادی آنهاBCC نام گرفت. مدلهای تحلیل پوششی داده ها به دو روش قابل ساخت هستند 1. روش مضربی 2. روش پوششی. در ادامه این دو روش و مدلهای مربوطه ارائه خواهد شد.
شاخص کارایی در حالت چند ورودی و چند خروجی به صورت نسبت مجموع وزنی خروجی ها به مجموع وزنی ورودی ها تعریف می گردد

در صورتی که بخواهیم کاراییn واحد که هر واحد دارای m ورودی وs خروجی باشد را حساب کنیم، کارایی واحد j ام (…n 1=j) به صورت زیر محاسبه میشود:
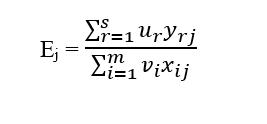
در مورد رابطه فوق باید به دو نکته توجه داشت: اول این که ارزش ورودیها و خروجیها میتواند متفاوت باشد و نتوان آنها را اندازه گیری کرد. دوم، ممکن است واحدهای مختلف به گونهای عملیات خود را سازمان دهند که خروجیهایی با ارزشهای متفاوت ارائه کنند، بنابراین به وزنهای متفاوتی در اندازه گیری کارایی نیاز است و در عمل محاسبه وزنها برای ورودی و خروجیهای مختلف کار سادهای نیست و در برخی از نمونههای کاربردی غیر ممکن است.
چارنز، کوپر و رودز این مشکل را شناختند و برای حل این مشکل مدلی را ارائه کردند که وزنها به عنوان متغیر در مدل تعریف میشود و با اجرای مدل مقادیر وزنهای ورودی و خروجی مشخص میشود.
برای ساختن مدل، فرض کنید n واحد موجود است و هدف، ارزیابی کارایی واحد تحت بررسی (واحد صفر یا واحد تصمیم گیرنده) است که ورودیهای xm,0 ,…, x2,0 , x1,0 را برای تولید خروجی های ys,0, …,y2,0, y1,0 مصرف میکند.
در صورتی که وزنهای تخصیص داده شده به خروجیها (یا قیمت خروجیها) با us, …, u2, u1 و وزن تخصیص داده شده به ورودیها (یا هزینه خرید ورودیها) با vs, …, v2,v1 نشان داده شود، برای پیدا کردن حداکثر کارایی، کسر زیر باید حداکثر شود.
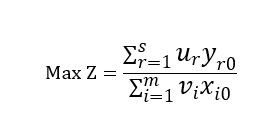
اگر U و V را متغیر در نظر بگیریم ماکسیمم کسر فوق بی نهایت میشود لذا برای جلوگیری از میل به بینهایت یک قید نرمال کننده به شکل زیر به مدل اضافه میکنیم.
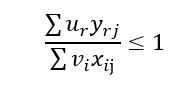
در نتیجه مدل زیر که به مدل کسری CCR معروف است به دست میآید.
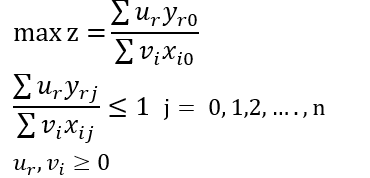
باید دقت کرد که تعداد محدودیتها در مدل کسری CCR برابر با تعداد واحدها و تعداد متغیرهای آن برابر با مجموع تعداد ورودیها و خروجیها ست. با توجه به تابع هدف و قیود، مشخص میشود که این مدل غیرخطی و غیر محدب است که با حل آن مقدار متغیرهای و برای اندازه گیری کارایی واحد تحت بررسی به دست میآید. مشکلی که در مدل سازی فوق وجود دارد آن است که این مدل کسری بوده و با نرم افزارهای حل مدلهای خطی قابل محاسبه نیست لذا این مدل با استفاده از تغییر متغیرهای مناسب به مدل خطی زیر تبدیل میشود که مدل خطی CCR نامیده می شود
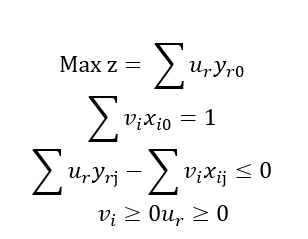
در سال 1984، بنکر، چارنز و کوپر با تغییر در مدل CCR مدل جدیدی را عرضه کردند که بر اساس حروف اول نام خانوادگی آنان به مدل BCC شهرت یافت. مدل BCC مدلی از انواع مدلهای تحلیل پوششی دادهها است که برای ارزیابی کارایی نسبی واحدها با بازده به مقیاس متغیر به کار می رود.
مدل کسری BCC برای ارزیابی کارایی واحد تحت بررسی به صورت زیر است:
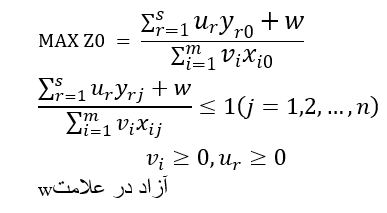
ساختار مدل کسری BCC همانند مدل کسری CCR است که هم در تابع هدف و هم در تمامی محدودیتها در صورت کسر، یک متغیر آزاد در علامت W افزوده میشود. این مدل نیز با استفاده از تغییر متغیرهای مناسب به صورت زیر به مدل خطی تبدیل می گردد.
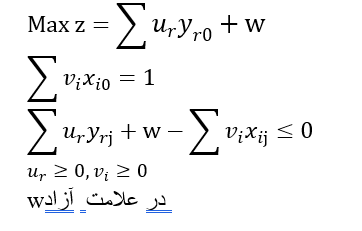
در فعالیتهای تولیدی، هر واحد تصمیمگیرنده (DMU) برداری از عوامل ورودی X
را مصرف می کند تا برداری از عوامل خروجی Y را تولید کند. ناحیه امکان تولید یا به اختصار PPS[1] که زیر مجموعهای از فضای R است به صورت زیر معرفی میشود:
این تعریف با توجه به نوع تکنولوژی تولید،PPS را مشخص میکند.
در مدلهای ناپارامتری فضای امکان تولید بر اساس DMU های مشاهده شده با استفاده از چند اصل بدیهی ساخته می شود
تمام DMU های مشاهده شده به مجموعه امکان تولید T تعلق دارند که آن را به صورت زیر نمایش میدهیم:
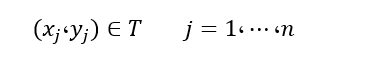

این اصل بیان میکند که اگر
به بیان سادهتر، هر افزایش (کاهش) متناسب در ورودیها باعث همان افزایش (کاهش) متناسب در خروجیها میشود.
T مجموعهای محدب و بسته است، یعنی اگر
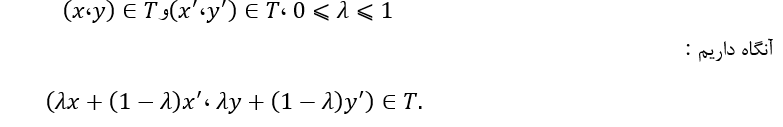
طبق این اصل Tc کوچکترین مجموعهای است که در اصول اول تا چهارم صدق میکند. در حقیقت، مجموعه امکان تولیدی که با چهار اصل فوق ساخته شود در اصل پنجم نیز صدق میکند.
ثابت میشود که اصول پنجگانهی بالا، مجموعهی منحصربه فرد را به صورت زیر تعریف میکنند.
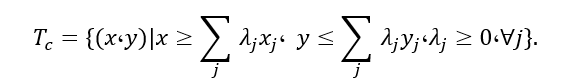
مجموعه با قبول اصل بازده به مقیاس ثابت ساخته شده است و علامت c نشانگر همین خاصیت است. با حذف بازده به مقیاس ثابت، مجموعه امکان تولید زیر ساخته میشود که دارای بازده به مقیاس متغیر است و به مجموعه امکان تولید BCC معروف است و با نمایش داده می شود