

تحليل سلسله مراتبي
در دنياي امروز با توجه به محدود بودن منابع و هزينه هاي گزاف آن، تصميم گيري درست در نحوه استفاده از منابع حائز اهميت است. چه بسا که يک تصميم گيري نادرست ممکن است به نتيجه مورد انتظار منجر نشده و سرمايه و زمان بسياري تلف شود. در پروژه ارزيابي عملكرد واحدها در لايه محاسبه شاخصها از AHP استفاده مي شود. در ادامه به ارائه كليتي از اين روش مي پردازيم.
بطور کلي فرايند تصميم گيري از لحاظ فضاي تصميم به دو دسته پيوسته و گسسته تقسيم مي شود و تصميم گيري در فضاي گسسته به دو دسته تک معياره و چند معياره تقسيم مي شود. خود معيارها به سه دسته معيارهاي کيفي، کمي و ترکيبي (کيفي و کمي) تقسيم مي شوند.
AHP متدولوژيي است که امکان تصميم گيري صحيح با حضور معيارهاي کيفي و کمي و ترکيبي را فراهم مي کند. پياده سازي AHP در يک تصميم گيري شامل 3 فاز است:
فاز 1: در فاز اول بايد عواملي که در تصميم گيري مهم مي باشند را در قالب يک درخت تصميم گيري بصورت سلسله مراتبي بيان کنيم بطور مثال تصور کنيد که از بين سه اتومبيل A ، B و C ميخواهيم يکي را انتخاب کنيم. در انتخاب اتومبيل چهار معيار قيمت ، مصرف ، سوخت ، راحتي و مدل مطرح مي باشند. درخت سلسله مراتبي براي اين مثال بصورت زير خواهد بود:
تحليل سلسله مراتبي
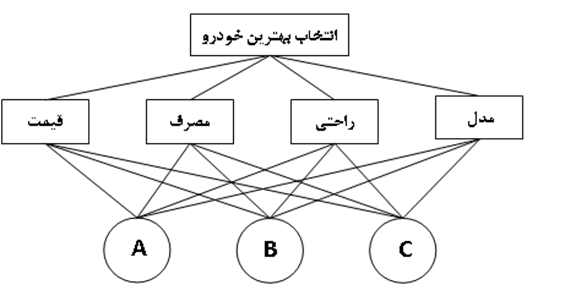
دقت کنيد که معيارهاي قيمت و مصرف معيارهاي کمي بوده و راحتي و مدل معيارهاي کيفي مي باشند.
در تحليل سلسله مراتبي براي هر کدام از گزينه ها يک امتياز بدست مي آوريم و گزينه ها بر حسب امتيازي که کسب کرده اند رتبه بندي مي شوند. مسلماً گزينه اي که بيشترين امتياز را کسب کرده بهترين گزينه براي انتخاب شدن است. روشي که در AHP براي محاسبه امتيازها بکار مي رود بر اساس مقايسات زوجي استوار است که در فاز دوم به شرح آن مي پردازيم.
فاز 2 : در تحليل سلسله مراتبي( مدل AHP) عناصر هر سطح نسبت به عنصر مربوطه خود در سطح بالاتر بصورت زوجي مقايسه شده و وزن آنها محاسبه مي گردد. اين وزنها را وزن نسبي مي ناميم سپس با تلفيق اين وزنها وزن نهايي هر گزينه مشخص مي شود. بطور مثال اگر بخواهيم اتومبيلها را بر اساس معيار راحتي مقايسه کنيم ابتدا اتومبيل A را با B از اين نظر مقايسه کرده و سپس A و C و بعد C و A را با هم مقايسه مي کنيم در اين مقايسه ها تصميم گيرنده ها از قضاوتهاي شفاهي استفاده مي کنند بگونه اي که اگر عنصر i با عنصر j مقايسه شود تصميم گيرنده خواهد گفت که اهميت I بر j يکي از حالتهاي زير است
ترجيحات | مقدار عددي |
کاملاً مهمتر | 9 |
مهمتر | 7 |
مهم | 5 |
کمي مهم | 3 |
يکسان | 1 |
البته از نظرات شفاهي و مقادير فوق هنگامي استفاده مي کنيم که شاخص کاملاً کيفي باشد و به هيچ وجه نتوان آن را از طريق شاخصهاي ديگري کمي کرد. بطور مثال شاخص زيبايي براي اتومبيل يک معيار کيفي است و براي محاسبه اين شاخص در مورد گزينه هاي مختلف ناگريز از بکارگيري روش فوق هستيم ولي شاخصهايي که مقادير کمي دارند مثل شاخص قيمت و مصرف را مي توانيم اندازه بگيريم و در مورد اين شاخصها از نظرات شفاهي استفاده نمي کنيم . در نظرات شفاهي يک نکته بايد در نظر بگيريم.
اگر اهميت عنصر i بر j برابر با n باشد ، اهميت j بر i برابر با است و با توجه به اين نکته کافي است در ماتريس زير فقط مقادير بالاي قطر اصلي را پر کنيم . مقادير زير قطر اصلي معکوس مقادير بالاي قطر خواهد بود به عبارت ديگر
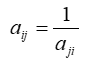
در مورد معيارها بايد به نوع آنها توجه داشته باشيم. مثلا معيار قيمت معياريست که کم بودن آن مطلوب بوده و معيار راحتي از نوعي است که زياد بودن آن مطلوب است. توجه به نوع معيار در روش محاسبه وزن آن اهميت دارد.
روش استخراج وزنها از ماتريس تصميم:
روش محاسبه وزنها از ماتريس تصميم به سازگار يا ناسازگار بودن ماتريس تصميم وابسته است .
اگر شرط
در ماتريس تصميم برقرار باشد مي گوييم که ماتريس تصميم سازگار است. همواره ماتريس تصميم اي که در مقايسه گزينه ها
نسبت به يک معيار کمي بدست مي آيند داراي اين خاصيت هستند اگر اين خاصيت برقرار نباشد ماتريس ناسازگار است که معمولاً ماتريسهايي که با استفاده از نظرات شفاهي توليد مي شوند ناسازگارند. براي هر نوع از ماتريسهاي تصميم روش خاصي در محاسبه وزنها وجود دارد که به تفکيک بيان مي کنيم.
ماتريس سازگار: در اين حالت اگر معيار از نوع Maximize باشد مولفه هاي يک ستون دلخواه از آنرا نسبت به مجموع آن ستون نرمال مي کنيم و وزنها بدست مي آيد اگر معيار از نوع Minimize باشد مولفه هاي يک سطر دلخواه از آن را نسبت به مجموع آن سطر نرمال مي کنيم و وزنها محاسبه مي شود.
ماتريس ناسازگار: در اين حالت از روش فوق نمي توان براي استخراج وزنها استفاده کرد. چهار روش عمده در محاسبه وزنها در حالت ناسازگاري ماتريس تصميم موجود است که عبارتند از:
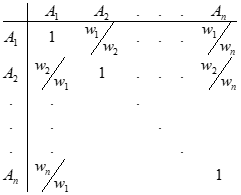
فرض کنيد وزن واقعي گزينه ها (W) باشد آنگاه ماتريس تصميم بايد به صورت زير باشد:
بايد w را بگونه اي پيدا کنيم که اختلاف مولفه هاي درماتريس فوق به کمترين مقدار ممکن برسد. براي اين کار مدل زير را بايد اجرا کنيم
تا
بدين ترتيب يک تقريب از وزنها بدست بیاید
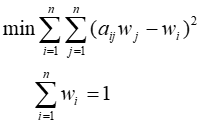
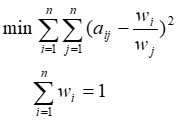
روش بردار ويژه : در اين روش بردار ويژه ماتريس تصميم به ازاي مقدار ويژه ماکسيمم به عنوان بردار وزن گزينه ها تعريف مي شود. محاسبه بردار ويژه يک ماتريس براي مقدار ويژه ماکسيمم از طريق يک الگوريتم تکراري محاسبه مي شود که ذکر جزئيات آن خارج از اين بحث است.
بعد از اينکه وزن هر گزينه را نسبت به هر معيار بدست آورديم وزن خود معيارها را نيز بطور مشابه نسبت به هدف محاسبه مي کنيم سپس وزن نهايي هر گزينه به صورت زير محاسبه مي شود.
که در آن w وزن گزينه I نسبت به معيار j و v وزن معيار j است.
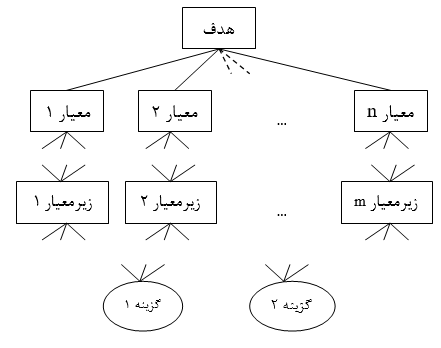
از قابليتهاي تحليل سلسله مراتبي( مدل AHP) اين است که معيارها مي توانند در قالب معيارهاي کلي و زير معيارها در چند لايه قرار بگيرند و لازم نيست عناصر لايه هاي مختلف به هم وصل باشند يا با توجه به ساختار مساله اين ارتباطها مي توانند تغيير کنند. حالت کلي يک درخت سلسله مراتبي را مي توان به صورت زير نشان داد
استفاده از نظرها و افکار ديگران خطاهاي تصميم گيري را تقليل داده و باعث بهبود کارها مي شود. با توجه به اينکه تصميم گيري در ادارات و سازمانها پيچيده است ممکن است تصميم گيرنده يک فرد نباشد و گروهي از تصميم گيرنده ها داشته باشيم در AHP امکان تصميم گيري گروهي وجود دارد . تعيين ماتريس تصميم در AHP تنها در مورد معيارهاي کيفي وابسته به نظر شفاهي و مقايسات زوجي تصميم گيرنده است حال اگر گروهي از تصميم گيرندگان وجود داشته باشند که بخواهند در مورد گزينه ها نسبت به يک معيار کيفي نظر دهند AHP اين امکان را فراهم مي کند که وزن نسبي گزينه را با استفاده از نظرات همه تصميم گيرندگان محاسبه کنند . روند کار بدين صورت است که در تشکيل ماتريس مقايسات زوجي اگر تصميم گيرندگان در يک مولفه ماتريس به توافق نرسند هر کدام مقدار مورد نظر خود را وارد مي کند . مقدار نهايي ميانگين هندسي آنها خواهد بود. ممکن است اهميت راي تصميم گيرندگان يکسان نباشد در اين حال گروه مي تواند در ابتداي فرآيند اهميت وزني هر عضو را تعيين کند.
تحليل سلسله مراتبي