

تحلیل پوششی داده ها (Data Envelopment Analysis) که به اختصار به آن DEA نیز گفته میشود، یک روش ناپارامتری در حوزه تحقیق در عملیات و اقتصاد در نظر گرفته شده که کار آن اندازهگیری یا برآورد کارایی عملکرد واحدهای تولیدی است. البته در اینجا منظور از واحد تولیدی میتواند شامل کارخانجات و همینطور شرکتهای ارائه کننده خدمات نیز باشد. در نتیجه میتوان از تحلیل پوششی داده ها در هر نوع فعالیتی اقتصادی استفاده کرد و کارایی واحدهای تصمیمگیری در آن حوزه را بدست آورد.
کارایی شاخصی است که توانایی مدیریت یک واحد تصمیم گیرنده را در استفاده بهینه از ورودی ها در جهت تولید خروجی ها می سنجد. هر چه یک واحد بتواند با مصرف ورودی کمتر خروجی بیشتری را تولید کند کارا تر است. توجه داشته باشید که بین دو واحد که میزان خروجی های مختلف تولید می کنند لزوما آنکه خروجی بیشتری تولید می کند ممکن است کاراتر از دیگری نباشد چون امکان دارد این واحد خروجی بیشتر را به واسطه استفاده از ورودی ها و امکانات بهتر و بیشتری از واحد دیگر تولید کرده باشد. لذا در بحث کارایی مقادیر ورودی ها و خروجی ها ملاک نیست بلکه نسبت آنها تعیین کننده است.
کارایی به عنوان نسبت خروجی به ورودی تعریف می شود و هر چه این نسبت در یک واحد بالاتر باشد به این معنی است که کارایی آن واحد بالاتر است. از آنجا که در عمل با واحد هایی مواجه هستیم که ورودی ها و خروجی های متنوعی را مصرف و تولید می کنند لذا محاسبه کارایی کمی پیچیده می شود با توجه به این نسبت یک واحد می تواند کارایی خود را با تولید خروجی بیشتر با بدون افزایش سطح ورودیش یا کاهش ورودی بدون کاهش سطح خروجی اش افزایش دهد. لذا تکنیکهایی برای محاسبه میزان کارایی و مقدار مناسب افزایش در خروجی و کاهش در ورودی به منظور رسیدن به کارایی صد درصد در سالهای اخیر ایجاد شده اند که عموما به دو دسته تکنیکهای پارامتری و تکنیکهای ناپارامتری تقسیم می شوند.
همه تكنيكهاي محاسبه كارايي بر اساس تابع توليد عمل مي كنند تابع توليد تابعي است كه بيشترين ستاده ممكن را به ازاي هر نهاده در يك سازمان مشخص مي كند. در حالت كلي روشهاي تعيين تابع توليد به دو دسته روشهاي پارامتري و روشهاي غير پارامتري تقسيم ميشوند. در روشهاي پارامتري كه در علم اقتصاد مورد استفاده قرار ميگيرد ابتدا يك فرم تابعي براي تابع توليد در نظر گرفته ميشود و سپس با استفاده از مقادير ورودي و خروجي پارامترهاي مجهول تابع برآورد ميشود. در روشهاي غير پارامتري هيچ فرم تابعي پيشفرض براي تابع توليد در نظر نميگيريم و تابع توليد بوسيله خود واحدها تعيين ميشود.
تكنيكهاي مختلفي به منظور محاسبه تابع توليد در روشهاي پارامتري ارائه شده است كه به دو دسته مدلهاي قطعي و مدلهاي احتمالي تقسيم ميشوند. در مدلهاي قطعي سعي در يافتن يك فرم تابعي (مرز توليد) داريم كه به ازاي هر مقدار ورودي بيشترين خروجي را دهد. فرض كنيد اين مرز يا همان تابع توليد با f مشخص شده باشد آنگاه
كه در آن yi ميزان خروجي واحد i ام، xi ميزان ورودي آن، β برداري از پارامترهاي تكنولوژيكي است كه بايد برآورد شود و TEi ميزان كارايي تكنيكي واحد i ام است.
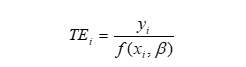
اين رابطه كارايي تكنيكي را به عنوان نسبت خروجي مشاهده شده به ماكسيمم خروجي شدني تحت تكنولوژي استفاده شده تعريف ميكند. هنگامي كه TEi=1 ، yi به بيشترين مقدار خود يعني f(xi , β) ميرسد و اگر TEi<1 ، yi مقداري كمتر از مقدار ماكسيمم قابل دسترس را دارد. در حالت اول واحد توليدي i ام كارا و در حالت دوم ناكارا است. يكي از توابع توليدي كه به عنوان تابع f استفاده ميشود تابع كاب-داگلاس است.
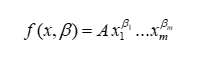
كه در آن xi ها ورودي و βi ها پارامترهاي تكنولوژيكي هستند كه بايد برآورد شوند. پارامترها را ميتوان با استفاده از مقادير مشاهده شده مربوط به واحدها از طريق روش كمترين مربعات برآورد كرد.
روشهاي پارامتري هم از لحاظ محاسباتي و هم از لحاظ منطقي محدوديتهايي دارند كه از جمله آنها ميتوان به موارد زير اشاره كرد.
در تلاش براي رفع مشكلات فوق روشهاي غير پارامتري ايجاد شدند. اين روشها از آن جهت غير پارامتري خوانده ميشوند كه پيشفرضي از شكل اساسي تابع توليد ندارند. فارل در سال 1957 اولين روش غير پارامتري جهت تعيين كارايي را در حالت دو ورودي و يك خروجي ارائه نمود. وي به جاي برآورد تابع توليد، مرز كاراي قطعه قطعه خطي را با اعمال فرضهاي زير با استفاده از تبديل يك به يك بدست آورد.
شيب پارهخطها، منفي يا صفر است.
هيچ واحدي بين مرز و مبدا قرار نميگيرد. به عبارت ديگر تمام نقاط مشاهده شده در سمتي از مرز قرار ميگيرند كه مبدا در آن واقع نباشد.
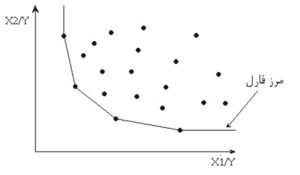
نقاطي كه روي مرز قرار ميگيرند نقاط كارا و بقيه ناكارا هستند و ميزان ناكارايي آنها به روشي كه در فصل قبل بيان شد محاسبه مي شود.
روش فارل با اينكه مشكل مربوط به انتخاب تابع توليد را رفع كرد ولي هنوز مشكل تعداد ورودي و خروجي را داشت. در سال 1978 چارلز و كوپر و رودز روش فارل را براي حالت چند ورودي و چند خروجي تعميم دادند كه به روش CCR معروف شد. در اين روش كارايي، مانند روشهاي پارامتري به صورت نسبت خروجي به ورودي تعريف شده و واحدي كه اين نسبت براي آن بيشترين باشد كارا ناميده ميشود.
فرض كنيد كه واحدها دراري چند ورودي و چند خروجي هستند. اگر ارزش وروديها و خروجيها را بدانيم آنگاه كارايي به سادگي به صورت زير قابل محاسبه است.
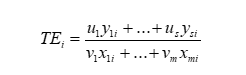
كه در آن vi ارزش ورودي و ui ارزش خروجي واحد i ام است. اما مشكل در تعيين ارزش وروديها و خروجيها است. اگر واحدهاي تحت ارزيابي، واحدهاي توليدي باشند ارزشدهي يا قيمتگذاري وروديها و خروجيها مشكل نيست اما اگر واحدها، توليدي نباشند تعيين ارزش واقعي وروديها و خروجيها مشكل و شايد غير ممكن باشد. مثلاً اگر براي يك مدرسه اگر ورودي را ميانگين معدل دانشآموزان هنگام ثبتنام و خروجي را تعداد قبولي در دانشگاهها در نظر بگيريم آنگاه ارزشدهي به اين نوع ورودي و خروجيها به طوري كه به خوبي بيانگر ميزان تاثير آنها در كارايي واحد باشد عملا غير ممكن است. لذا در روش CCR ارزش وروديها و خروجيها متغير فرض شده و براي محاسبه كارايي برنامه كسري رو برو ارائه شد.
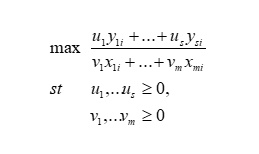
اين برنامه بدون هيچ فرض ديگري بيكران است لذا يك فضاي مقايسهاي در قالب قيود به شكل زير به برنامه اضافه شد.
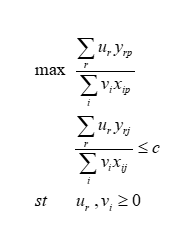
c يك ثابت دلخواه است كه معمولاً يك فرض ميشود. در واقع برنامه فوق تمام ارزشگذاريهاي ممكن را براي ورودي و خروجيهاي واحد p ام در نظر ميگيرد و ارزشهايي را مييابد كه به ازاي آنها تابع هدف بيشترين شود. با توجه به قيود مساله فوق، مقدار تابع هدف حداكثر c ميتواند باشد. حال اگر واحد p ام نسبت به بقيه واحدها ناكارا باشد در روند بيشينه كردن تابع هدف قيدهاي مربوط به واحدهاي كارا در مجموعه قيود زودتر به مقدار c ميرسند و واحد p ام را مجبور ميكنند در سطحي زير c قرار بگيرد ولي اگر واحد p كارا باشد تابع هدف به مقدار c مي رسد بدون اينكه شدني بودن قيود از بين برود.
تعبير ديگري كه براي مدل CCR ميتوان در نظر گرفت اين است كه مدل CCR را ميتوان به يك بازار تشبيه كرد كه در آن واحد تحت ارزيابي p ميتواند وروديهايش را به هر قيمتي بخرد و خروجيهايش را به هر قيمتي بفروشد اما واحدهاي ديگر نيز ميتوانند ورودي و خروجيهایشان را به قيمتهايي كه واحد p معامله ميكند، معامله كنند. حال در اين بازار رقابتي واحدي كارا است كه نسبت ميزان فروش به ميزان خريد براي آن بيشترين شود. لازم به ذكر است كه مدل CCR بيان شده در فوق كسري است و در عمل از خطي شده آن استفاده ميشود. در ادامه برخي از مدلهاي پر كاربرد تحليل پوششي داده ها را بيان مي كنيم
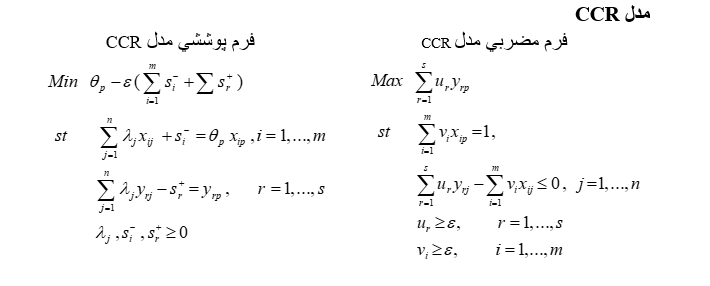
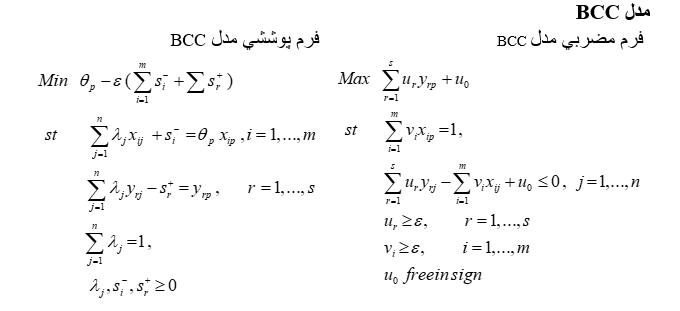
مدلهاي فوق همگي مدلهاي با ماهيت ورودي هستند. يعني مرز كارا را در جهت مينيمم كردن ورودي تا جايي كه خروجي كاهش نيابد مييابند. نظير همين مدلها را با ماهيت خروجي ميتوان نوشت. مدلهاي با ماهيت خروجي مرز كارا را در جهت ماكسيمم كردن خروجي تا جايي كه ورودي افزايش نيابد محاسبه ميكنند. مدل ديگري به نام مدل جمعي نيز وجود دارد كه در آن جهت بهينگي تركيبي از دو جهت فوق است.

در سالهای اخیر مدلهای دیگری نیز در مبحث مدلهای DEA معرفی شده اند که امکان به کار گیری محدودیت های وزنی را در مدل فراهم می کند. مدلهای کارایی نسبی پادینوسکی از این جمله اند.
مدلهای دیگری نیز برای محاسبه رشد بهره وری در طی سالهای مختلف فعالیت واحدها موجود است که از جمله آنها می توان از اندیس مالمکوئیست نام برد. با استفاده از این مدل رشد ایجاد شده در فعالیت یک واحد در هر سال به رشد در تکنولوژی و رشد در کارایی تفکیک می شود.